The Fibonacci numbers are the sequence of numbers 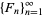defined by the linear recurrence equation

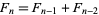 ![ F_n=F_(n-1)+F_(n-2) ](http://mathworld.wolfram.com/images/equations/FibonacciNumber/NumberedEquation1.gif)     with 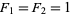![F_1=F_2=1](http://mathworld.wolfram.com/images/equations/FibonacciNumber/Inline2.gif) and 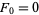![F_0=0](http://mathworld.wolfram.com/images/equations/FibonacciNumber/Inline3.gif)

So in simple terms a method to compute fibonacci number for nth place looks like this

     if n == 0 or n ==1:
         return n
     else:
        return fibonacci(n-1)+fibonacci(n-2) 

here is quick test

    print i," : ",fibonacci(i)


#This will print
0  :  0
1  :  1
2  :  1
3  :  2
4  :  3
5  :  5
6  :  8
7  :  13
8  :  21
9  :  34

or an inline method like this print [fibonacci(i) for i in range(11)] will result

Running time of fibonacci series is quite interesting. The first version using recursion has a very bad polynomial time (one can try seeing the performance degrade by passing in larger numbers like 30) so ```def fab(n):
if n == 0 or n ==1: return n else: return fab(n-1)+fab(n-2)

#This would take polynomial time, (3.4)seconds on my macbook. fab(35)

 There is a better way of doing this in linear time

 ```def fab2(n):
    if n == 0:
     return 0
    f = [0 for j in range(n+1)]
    f[0] = 0
    f[1] = 1
    for i in range(2,n+1):
        f[i] = f[i-1]+f[i-2]
    return f

#this will print the sequence in linear time less than 0.1 seconds
fab2(35)

Few days ago I found another interesting way to code this using enumerate and yield in python

   a, b = 0, 1
   while True:            # First iteration:
       yield a            # yield 0 to start with and then
       a, b = b, a + b    # a will now be 1, and b will also be 1, (0 + 1)

and usage

    print('{i:3}: {f:3}'.format(i=index, f=fibonacci\_number))
    if index == 10:
        break

prints

 1:   1
 2:   1
 3:   2
 4:   3
 5:   5
 6:   8
 7:  13
 8:  21
 9:  34
10:  55

Here are some interesting facts about the Leonardo Fibonacii.