basic sorting algorithms implemented in golang
This post includes go-lang based implementation of some of the classic sorting algorithms.
This article primarily, has been written, as an academic exercise, to not forget the basic principles of sorting.
Bubble Sort
Bubble sort is perhaps the simplest of all sorting algorithms, the basic principle is to bubble up the largest (or the smallest) and then the second largest and then the third largest and so on. Each bubble takes the full sweep of the list, hence best-case, average-case as well as the worst-case performance are all O(n2)
func BubbleSort( items []int) {
L:=len(items)
for i:=0;i<L;i++{
for j:=0;j< (L-1-i);j++{
if items[j] > items[j+1]{
items[j], items[j+1] = items[j+1], items[j]
}
}
}
}
Insertion Sort
Insertion sort takes each element through the list and inserts it at the right place. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain. Worst-case and average-case performance is O(n2), however the best case is O(n).
func InsertionSort(items []int) {
L := len(items)
for i := 1; i < L; i++ {
j := i
for j > 0 && items[j] < items[j-1] {
items[j], items[j-1] = items[j-1], items[j]
j -= 1
}
}
}
Merge Sort
Mergesort operates by diving the list into two sublist recursively till each sublist contains only one element, it then merges the adjacent list back while sorting each element in the merged list. Best-case, average-case as well as the worst-case eprformance are all O(nlogn)
const NADA int = -1
func DeepCopy(vals []int) []int {
tmp := make([]int, len(vals))
copy(tmp, vals)
return tmp
}
func MergeSort(items []int) {
if len(items) > 1 {
mid := len(items) / 2
left := DeepCopy(items[0:mid])
right := DeepCopy(items[mid:])
MergeSort(left)
MergeSort(right)
l := 0
r := 0
for i := 0; i < len(items); i++ {
lval := NADA
rval := NADA
if l < len(left) {
lval = left[l]
}
if r < len(right) {
rval = right[r]
}
if (lval != NADA && rval != NADA && lval < rval) || rval == NADA {
items[i] = lval
l += 1
} else if (lval != NADA && rval != NADA && lval >= rval) || lval == NADA {
items[i] = rval
r += 1
}
}
}
}
Quicksort Sort

Quick sort works by first selecting a pivot element from the list. It then creates two lists, one containing elements less than the pivot and the other containing elements higher than the pivot. It then sorts the two lists and join them with the pivot in between. Just like the Merge sort, when the lists are subdivided to lists of size 1, they are considered as already sorted. Best-case and avergae-case is O(n log n) however the worstcase(very rare) is O(n2)
if len(items) > 1 {
pivot\_index := len(items) / 2
var smaller\_items = []int{}
var larger\_items = []int{}
for i := range items {
val := items[i]
if i != pivot\_index {
if val < items[pivot\_index] {
smaller\_items = append(smaller\_items, val)
} else {
larger\_items = append(larger\_items, val)
}
}
}
QuickSort(smaller\_items)
QuickSort(larger\_items)
var merged []int = append(append(append([]int{}, smaller\_items...), []int{items[pivot\_index]}...), larger\_items...)
//merged := MergeLists(smaller\_items, items[pivot\_index], larger\_items)
for j := 0; j < len(items); j++ {
items[j] = merged[j]
}
}
}
Heap Sort
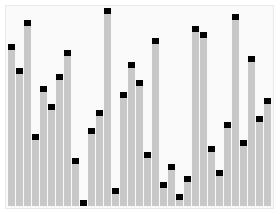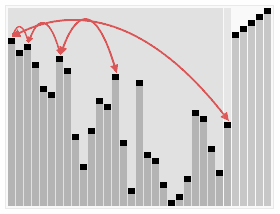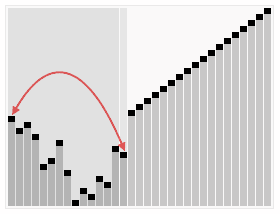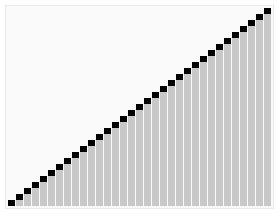
Heapsort can be thought of as an improved selection sort: like that algorithm, it divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. The improvement consists of the use of a heap data structure rather than a linear-time search to find the maximum,best-case, average-case as well as the worst-caseeprformance are all O(nlogn)
func heapify(items []int, idx int, size int) {
l := 2*idx + 1 // left = 2*i + 1
r := 2*idx + 2 // right = 2*i + 2
var largest int;
if l <= size && items[l] > items[idx] {
largest = l
} else {
largest = idx
}
if r <= size && items[r] > items[largest] {
largest = r
}
if largest != idx {
t := items[idx]
items[idx] = items[largest]
items[largest] = t
heapify(items, largest, size)
}
}
func HeapSort(items []int) {
L := len(items) //heap size
m := int(L / 2) //middle
for i := m; i >= 0; i-- {
heapify(items, i, L-1)
}
F := L - 1
for j := F; j >= 0; j-- {
t := items[0]
items[0] = items[j]
items[j] = t
F -= 1
heapify(items, 0, F)
}
}
Finally to run these algos I have written a quick main program
"fmt"
"time"
"math/rand"
)
func main() {
fmt.Println("Preparing!")
var randomVals = []int{}
s1 := rand.NewSource(time.Now().UnixNano())
r1 := rand.New(s1)
for i := 0; i < 11; i++ {
randomVals = append(randomVals, r1.Intn(99)+1)
}
fmt.Println("Unsorted!")
fmt.Println(randomVals)
//BubbleSortrandomVals()
//InsertionSort(randomVals)
//MergeSort(randomVals)
//QuickSort(randomVals)
HeapSort(randomVals)
fmt.Println("sorted!")
fmt.Println(randomVals)
}


